１．研究分野について

私の主な研究分野は4次元トポロジーです。4次元トポロジーとは、ざっくりいうと4次元多様体やその部分多様体の（トポロジカルな）性質を研究する分野のことです。なお次元が4以下の対応する分野はまとめて低次元トポロジーと呼ばれています。4次元トポロジーと一口に言っても様々な分野がありますが、私は4次元多様体の微分構造（即ち微分同相による同値類）の研究を中心に行っています。また4次元トポロジーの周辺分野への応用にも取り組んでいます。

２．多様体の位相構造と微分構造について

上のように書くと、なぜ一般の次元ではなく4次元に絞って研究するのか？と思われる方も多いでしょう。4次元は非常に特殊な次元で、他の次元の手法が適用できない様々な困難が存在するため、他の次元と違い解明されていないことが非常に多いのです。そのため4次元に固有の研究手法を発展させる必要があります。

まず2次元以下の多様体については古典的によく知られています。例えば有向2次元閉多様体の位相構造（即ち同相による同値類）は種数（穴の数）によって完全に分類されます。3次元多様体の位相構造は非常に難しいのですが、基本群によって統制されていることが知られています。特に難しいのが3次元球面の位相構造の特徴付けでした。20世紀初頭に提出されたポアンカレ予想「単連結閉3次元多様体は3次元球面と同相である」がペレルマンによって解決されたニュース（そしてその後のフィールズ賞辞退）は、数学に興味のない方ですら耳にしたことがあるのではないでしょうか（2006年頃の話なので若い方はご存じないかもしれませんが）。しかしそもそも3次元以下の次元では、微分構造はその下部構造である位相構造によって一意に決まることが知られているため、微分構造の研究は位相構造の研究に帰着されます。

4次元以上になると位相構造はさらに複雑で、同じ基本群を持つ多様体が山のように存在します。特に任意の2つの閉多様体が同相か否か判定するアルゴリズムは存在しないことが知られています。その上、4次元以上では微分構造が位相構造から一意に定まるとは限りません。中でも4次元はユークリッド空間Rnがエキゾチック（即ち同相だが微分同相でない）微分構造を持つ唯一の次元であるなど、4次元特有の様々な興味深い現象が知られています。また5次元以上と異なり、4次元ではその上の微分構造が分類されているような位相構造は未だに一つもなく、微分構造に関しては最も難しい次元と言えます。

３．具体的な研究内容

ここでは私の研究分野について、どのような方法で研究が進められているのか具体的に説明します。私が修士のときのセミナーで学んだのは主に4次元ハンドル体の図式（Kirby図式）ですが、現在でも私の主要な研究道具の一つですのでこれについて紹介します。

３.１．ハンドル体について

まず簡単にハンドル体の説明をしておきます。k次元球体（つまり原点からの距離が1以下のRkの元の集合）をDkと表し、多様体Xの境界を∂Xで表すことにします。n次元ｋハンドルとはDk×Dn-kのことを言います。ｋハンドルを（境界付き）ｎ次元多様体Xに接着するとは、∂Dk×Dn-kから∂Xへの埋め込み写像を用いることによって、∂X の（余次元0）部分多様体とkハンドルの境界の一部である∂Dk×Dn-kを同一視し、kハンドルとXを貼り合わせる操作のことをいいます。図１は2次元円板D2（緑の円板）に1ハンドル（青い長方形）を接着した様子を図示したものです。

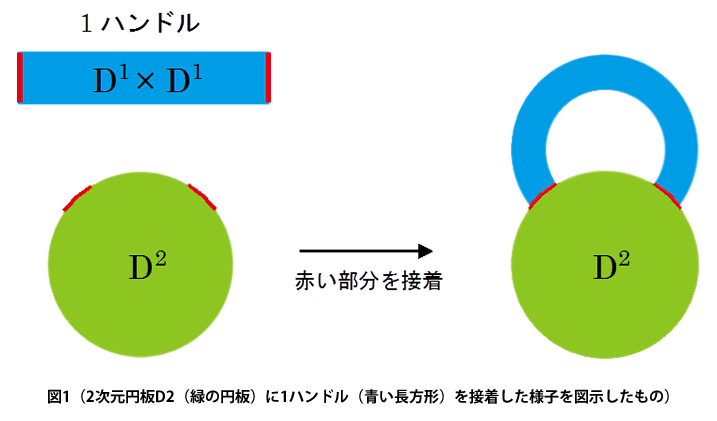
そして0ハンドルD0×Dn（即ちｎ次元球体Dn）にハンドルを次々と貼り付けて得られる多様体のことをｎ次元ハンドル体と言います。任意のコンパクトなｎ次元可微分多様体はｎ次元ハンドル体に分解できるので、多様体の（トポロジカルな）性質を調べたければ、ハンドル体の性質を調べればよいことになります。なお3次元以上では各ハンドルの接着の仕方が無数にあり、一般にハンドル体は非常に複雑です。

次元が高くなるとハンドル体は図１のようには直接図示することができませんが、３、4次元の場合は各ハンドルの接着写像の情報を取り出すことによって間接的に図示することができます。4次元の場合そのような図式はKirby図式、ハンドル体図式などと呼ばれています。図式の具体例は次の節で紹介しますが、結び目や絡み目と整数を使って表されます。ハンドル体を使うと、目で直接見ることのできない4次元多様体の様々な性質を、図式から論理と想像によって読み取ることができ、多様体を手で直接触って調べるような楽しさがあります。

３.２．4次元ハンドル体と微分同相

4次元ハンドル体やその図式の応用には様々なものがありますが、最も典型的なのは、見かけ（構成の仕方）が全く異なる２つの4次元多様体が微分同相であることを示すことです。ハンドル以外の方法では全く証明できないことがしばしばあります。2つのハンドル体の図式がある種の変形操作で移りあうことを絵で描いて示せば良いのですが、変形の自由度が高すぎるので一般には非常に困難です。しかし、初等幾何の問題で良い補助線を見つけるときのような楽しさが味わえることもあります。例として次の論文の結果を紹介します。

　[A] S. Akbulut, Cappell-Shaneson homotopy spheres are standard, Ann. of Math. (2) 171 (2010), no. 3, 2171-2175.

図２はこの論文でΣmと呼ばれている、4次元球面S4と同相な4次元多様体のハンドル体の図式です（ｍは整数）。黒丸がついている2つの結び目（閉じた紐のこと）はそれぞれ1ハンドルを表していて、そばに「０」、「１」の数字がついている2つの結び目はそれぞれ2ハンドルを表しています（左上のボックスは３．本の線が(－m)回捻られていることを表しています）。各ΣmはCappellとShanesonの1976年の論文で（ハンドルを使わずに）定義された4次元多様体で、長い間エキゾチックS4（即ちS4と同相だが微分同相でない多様体）の候補として注目されていました。m=0の場合は1991年にGompfがエキゾチックS4ではないこと（即ちS4と微分同相であること）を、ハンドル体の図式を使って鮮やかに証明しました（2、３．ハンドル対の生成を上手く使う）。しかしその他の場合はずっと未解決のままでした。その後2009年にFreedman、 Gompf、 Morrison、 Walkerはm≠0の場合にエキゾチックであることを示すための興味深い新しいアプローチ（結び目不変量を使う）をarXivで発表しました。しかし驚くべき事にAkbulutはそのわずか数日後に論文（たった5ページ）をarXivで発表し、全てのmについてエキゾチックでないことを証明しました。前述のGompfの方法を発展させた鮮やかな証明です。但し、一般に微分同相であることを示す研究は常にこのような鮮やかな方法で行われているわけではなく、暗闇の中を手探りで進んでいくような変形が必要になることもあります。

３.３．私の研究について

私は上で述べたような微分同相であることを示す研究も行っていますが、私がハンドル体（とその図式）を用いて主に研究しているのは、エキゾチック微分構造など新しい性質を持つ４次元多様体の構成や、（ゲージ理論やシンプレクティック幾何などの諸結果と組み合わせることにより）4次元多様体への様々な制約を与えることです。また周辺分野への応用にも取り組んでいます。ここでは下記の私の論文の結果について簡単に紹介します。

　[Y] K. Yasui, Corks, exotic 4-manifolds and knot concordance, preprint, arXiv:1505.02551 (2015).

枠付き結び目（即ち結び目と整数の組）は4次元ハンドル体を経由することで境界付き4次元多様体を自然に与えます。そのため、エキゾチックな（即ち同相だが微分同相でない）4次元多様体の対を表示する枠付き結び目の対の存在問題が自然に考えられますが、枠が±１の場合しか存在が知られていませんでした。私は上記の論文で、全ての枠に対し、エキゾチックな4次元多様体の対を表示する枠付き結び目の対を組織的に構成する方法を与えました。さらに枠が0の場合のこの結果を結び目理論の問題に応用し、1978年に提出されたAkbulutとKirbyの予想「2つの結び目が0手術で同じ3次元多様体を与えるならば、それらはコンコーダントである」に対する初の反例を与えました。図３の結び目の対がその一例です。私の他の研究については具体的な説明は省略しますが、私の論文はMathSciNetやarXivで調べることができます。

４．参考文献

4次元トポロジーの参考文献のうち、私の研究と関係の強いものに絞っていくつか紹介します。

[1] 松本 幸夫、『4次元のトポロジー』、日本評論社、2016年

4次元トポロジーの面白さがよくわかる本です。初版は1979年に出版されていて、9章、10章、第∞章で4次元トポロジーが扱われています。第∞章「“４次元”とは何だろう」では当時行われた４次元トポロジーの座談会の様子が掲載されています。1980年代に登場したFreedman理論、Donaldson理論という４次元トポロジーの２大理論（どちらの理論もフィールズ賞受賞！）が現れるわずかに前の時期に座談会は行われたようで、これらの理論が登場したずっと後で４次元トポロジーを学び始めた私には非常に興味深いです。これまでに数回改訂されていますが、各改訂時の4次元トポロジーの現状が付録やあとがきとして書かれているので、4次元トポロジーの発展の様子を当時の状況とともにうかがい知ることができます。

[2] R.E. Gompf and A.I. Stipsicz, “4-manifolds and Kirby calculus”, Graduate Studies in Mathematics, 20, American Mathematical Society, 1999

この本は4次元トポロジーの非常に有名な教科書で、ハンドル体とその図式（Kirby図式）、様々な手術、Lefschetzファイバー空間、シンプレクティック多様体、シュタイン多様体、ゲージ理論、など4次元トポロジーの様々なトピックが扱われています。多数の演習問題が出題されていますが、重要なものは巻末に丁寧な解答がついています。この本を読めば（全部読み通さなくて良いですが）、すぐに研究に取りかかれます。私が修士のセミナーで読んだのはこの本です。

[3] B. Ozbagci and A.I. Stipsicz， “Surgery on contact 3-manifolds and Stein surfaces”, Bolyai Society Mathematical Studies 13, Springer-Verlag, Berlin; Janos Bolyai Mathematical Society, Budapest, 2004

4次元多様体のシュタイン構造やその境界の3次元多様体の接触構造について、主にトポロジカルな視点から書かれた本です。低次元トポロジーとシンプレクティック幾何にまたがる分野であり、様々な応用があります。

[4] S. Akbulut, “4-manifolds”，Oxford Graduate Texts in Mathematics 25, Oxford University Press, 2016

ごく最近出版された4次元トポロジーの本です。この本も[2]と同様に4次元トポロジーの様々なトピックを扱っていますが、15年以上後に出版されているのでごく最近の話題も含んでいます。著者は私の共同研究者で、私との共同研究もこの本では扱われています。

５．博士前期課程で私の研究室に配属を希望される方へ

博士前期課程では4次元トポロジーの勉強・研究をして頂こうと考えています。まず上記の[2]，[3]，[4]のいずれかをテキストとしてセミナーを進めてもらうつもりです。テキストをある程度読んだ後、各自の興味に応じた論文を読んでもらい、研究に取り組んでもらう予定です。なおこれらの本では、多様体、特異ホモロジー（切除定理とMayer-Vietoris完全系列まで）、基本群、位相空間、線型代数、加群、を特によく使うので、入学前に勉強・復習しておいて下さい。余力があればさらに、ベクトル束、特性類、結び目などに関する基礎を学んでおくと良いと思います。