どんな分野の研究をしているのか

これまでの経験を分析して未来を予測すること、あるいは望ましい挙動を示すように系を構築することは様々な分野の研究において重要な位置を占める課題です。このために広く用いられる手段の一つとして、状態の時間変化が与えられた規則に従うとする数理的なモデルを用いた研究があります。モデルは現実の世界を何らかの形で単純化したものですが、モデルの選び方によっては必ずしも目的とするシステムの振る舞いを再現できるとは限りません。よりよいモデルを手に入れるためには時間発展の規則とそこから導かれる系の挙動との間の関係を理解することは重要になると考えられます。時間発展の規則とそこから生じる挙動の関係は必ずしも単純ではなく、環境を一定に保った系においても周期的な振動や不規則な揺らぎが自発的に現れたりします。系の状態が複雑に変化している場合、それは外部環境が複雑に変化したためである可能性はもちろん考えられますが、系が従う時間変化の規則により自発的に作り出されているという可能性も考えられます。そのため、時間変化を伴う現象について理解する上では、様々なモデル系がどのような時間変化を伴う挙動を示し得るのかを知っておくことが必要になります。計算機の発達とともに多数の変数を持つ複雑なモデル系が様々な分野で用いられるようになる中、大自由度の力学系についてさらに深く研究していく必要があると考えています。

興味の方向性とテーマ

私自身についていうと、いろいろなシステムの時間変化に伴って現れるさまざまな現象のメカニズムを解明することが研究の直接的なきっかけとなることも多いのですが、直接研究の対象としている力学系はそれ自体は抽象的な「数の世界」に属するものですし、目指している目標としてはある種の力学系が普遍的にもつ構造を明らかにするという基礎的な部分を指向したものがあります。研究を進める上では、具体的に作業系を設定してその挙動を計算機を用いて調べ、その観察結果を元に仮説の構築・検証を行うといった、実験系の研究に近いアプローチが大きな部分を占めています。比較的単純で現実の系とも対応するような規則を持つ系において観測される現象の裏に、いたる所不連続な構造や無限の繰り返し構造等、現実離れしたようにも思われるほど複雑な数学的構造が隠れているのを見ることができたりするのが面白いところだったりします。

テーマとして、これまでに扱ってきた主なものをあげると次のようなものになるかと思います。ただ、入り口として考える系や現象がなんであっても、面白い現象を生み出すメカニズムの根本的な部分を探っていくと、系の詳細にはよらない一般的な構造が見えてくることはあります。というわけで、扱う系についても特に下のようなものに限って考えているわけではありません。

－大自由度の写像系の振舞いとその機構－\(^*\)

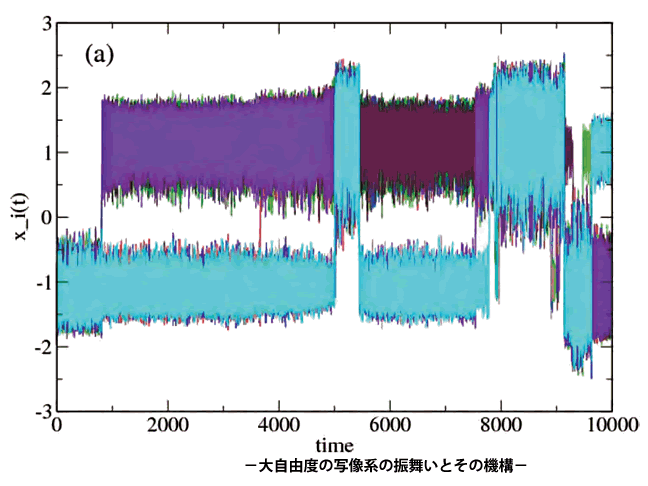
１次元あるいは２次元の実区間上で定義された単純な写像系は、カオスの研究においてとても大きな役割を果たしてきました。こういった少数次元の力学系で見られるものとは本質的に異なる構造について知ろうとするときに有望な作業モデル系の一つとして「結合写像系」といわれるような大自由度の写像系があります。

この系が示すいろいろな振舞いについては、特に数値実験を用いていろいろな角度から調べられて、いろいろな面白い現象が見つかっていますが、その機構の部分は謎のままになっているものがいろいろとあります。その中でも特におもしろい現象としては、多数の要素がからなる系が、個々の要素とは全く異なる集団としての挙動を示すという現象があります。一見個々の要素の振る舞いとは大きく異なる集団としての挙動がどのようにして作り出されているのかという機構について研究しています。

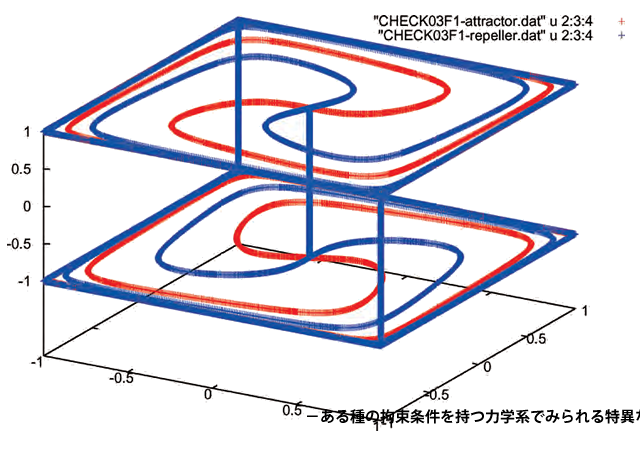
－ある種の拘束条件を持つ力学系でみられる特異な構造－

様々なシステムやそこで見られる現象に対応するモデル系として力学系を考える場合、元の系がもつ対称性や保存則といった性質を反映した力学系を考えるのが自然であろうと思われます。このような力学系はある意味「特殊」な力学系ではあるのですが魅力的な研究の対象です。

例えば、いろいろな生物の個体数の増減を生物間の相互作用を取り入れて記述する生態系の個体数変動のモデルは、それ自体非線形の力学系の研究のなかでも重要な役割を果たしてきています。多くの種が含まれるような系において見られる現象には、多様な種が共存する生態系の成り立ちを考える上でも、また大自由度の非線形力学系の持ちうる構造を考える点でも、それぞれ興味深い点があり、研究の対象として考えています。

実際には主にどんなことをやっているのか

計算機を使って行う数値実験のなかで現れる謎の現象が、どのような機構で起きるのかを調べる。ということをやっています。

のように状態の時間変化をあらわす写像を繰り返し作用させて、その結果えられる点列を時系列をあらわすもの（軌道）としてみなすというようなものです。

基本的に扱う系は初期条件を与えるとその後の軌道は一意に決まってしまうようなものですから、数値実験といっても計算機は与えられたルール（プログラム）にしたがって計算を行い結果を出してきます。そういう意味では「実験」するまでもなく結果は決まっていて、「謎の現象」の入り込む余地などないように思うかもしれません。しかし実際には時間発展のルールをみればそこからすべてがわかるような系はむしろほんの一握りの例外的なもので、大概のシステムの振る舞いには謎が残っています。ちょっと状態空間の次元が大きくなるともうわけがわからないことだらけで、どこから手を付けてよいのかもわからないくらいのことも多いのです。こういったわけがわからない系に対しては、数値計算の結果はやってみないことにはわからないまさに「実験」です。

一見わけがわからない振る舞いをする系に対して「こうやって見てみるともしかしたら何かわかるかもしれない」という切り口を考えてみたりしながら、いろいろな実験をしてみてその結果を観察することで手がかりとなると思われる規則性や特徴を探し、さらにその規則性の正体を見極めるために工夫して実験を行ったり、何が起きているかを考えて仮説をたてそれをいろいろな方法で確かめる。というようにして研究を進めていって、何らかの形で今まで誰も知らなかった知識を手に入れることを目指す、というようなことをやっています。

大学院生の研究について

上にも少し書いたように、非線形のダイナミクスの研究にはいろいろな側面があります。普遍性を持った基礎的な構造や概念を定式化していく、計算機実験を用いてモデル上でのいろいろな現象を観察していく、あるいは生物等も含むいろいろな実際世界で見られる現象を題材としてその奥にある動力学的構造を調べるなど、人により目指す方向もいろいろだと思います。どういう方向を目指すにしても、力学系についての基本的な関する理解と計算機実験をするための基本的なプログラミング等は勉強していく必要があります。ということで、多分最初にカオスに関する部分に重点をおいた力学系のテキストを読んだ後、具体的なテーマについて考えていくということになると思います。

研究するテーマについては、ある程度具体的な現象に関係するものについて、いろいろな計算機実験をしていくというものを希望する学生さんが多いです。その場合題材は必ずしも上で挙げたようなものとは限らず、自分で興味を持った現象について研究してもらえればと思います。自分で興味を持った面白そうな何か、をとっかかりとしていろいろ調べていくと、多分同じような疑問を抱いて調べた他の人の論文を読むことになります。それらを理解するために勉強するなかで必要な知識を身につけ、また疑問点を整理してさらに調べていくというようにして進んでいくことになるでしょう。ある意味とても混沌としたところのある研究分野ですし、研究をスタートする時点では十分な基礎知識があるわけではないので、最初の予定通りに進まずに予想していなかった方向に進んでいくことはよくあります。そういう意味では現象論的な方向で研究をしていくつもりであっても、場合によってはかなり基礎的な部分について研究することが必要になったり、その逆になることもあると思います。

いろいろな試行錯誤が避けられない「手探り」での研究という要素が強く、ある程度「なんでも屋」として研究していくことでこの分野の面白さを味わうことができるのではないかと思います。そういったわけで、謎解きのための試行錯誤を楽しむことができて、数学と計算機が好きな学生さんが来てくれることを希望しています。

その他（こういう研究をするようになった経緯など）

私自身が最初に扱ったテーマは神経細胞の集団的な挙動に関する研究でした。対象とした現象は、大脳のある領野において多数の神経細胞が同期して活動するという現象が観測され、さらにその同期の範囲が与えた刺激の特徴をよく反映したものになるというものです。これだけ書いてもなんのことやら？という事になってしまいますが、脳内での情報処理に神経細胞の活動の大きさ（発火の数）だけではなく、活動のタイミングが重要な役割を果たしている可能性を示すものとして、大きな関心を呼んだ現象です。この現象に対して、なるべく単純でありながらその振舞いを定性的に再現するような数理的なモデルを構築していくという現象論的な立場からの研究で一応の結果を得ることができました。

この研究では、脳で行われている複雑な情報処理の仕組みを（実際の神経細胞よりは遥かにその振舞いがわかりやすいような）微分方程式などのモデルを用いて調べることにより明らかにしていくということを目指しているわけですが、最初の実験で扱っていた比較的単純な処理の部分から研究を先に進めてより複雑な高次の処理について考えていこうとすると大きな問題に突き当たりました。神経細胞の活動のような比較的具体的な観測の対象となる現象と、そこでの情報処理というある意味漠然とした高次の機能というものの間には大きなギャップがあります。微分方程式系などを使って表されるようなモデルを使うことによりこのギャップを埋めていくというのが大きな目標のわけなのですが、高次の機能に相当するような複雑さを持った現象が、微分方程式といった力学系の枠組みのなかでどのように表現されうるのか、という点についてはあまりにもわからないことだらけでした。たくさんの神経細胞がもうちょっと複雑な処理をするような場合に対応するような数値実験をすることが仮にできたとして、その大量のデータをどのようにして見ればモデル系のなかで起きていることを理解できるのか、という部分がさっぱりわからないわけです。これではモデルを使って計算機実験して、それっぽい現象の再現ができたとしてもいまひとつうれしくありません。ともかくももう少し大自由度の力学系というものにたいする理解を持たないことには先へ進むのは難しいということで、大自由度の力学系についていろいろと調べているうちにこれはこれで面白い問題が出てきて色々と調べてきたということになるかと思います。大自由度力学系とは言っても具体的に取り組んできた対象の選択は実際のところかなり行き当たりばったりだったりするのですが、後から見ると色々なテーマの奥にはつながりが見えてきたりしてこれはこれで面白いと感じています。