1. 研究分野について

私は「数値解析学」と呼ばれる分野の研究を行っています。

現代科学の多くの問題は、紙と鉛筆で解析的に解を求められることは極めて稀であり、コンピュータを用いた数値計算（シミュレーション）が必要不可欠です。 数値計算を行うためには、数値解法が必要です（数値計算手法、あるいはアルゴリズムと呼ばれたりします）。すなわち、必要に応じて問題の近似などを行ったうえで、具体的な計算の手順を指示する必要があります。しかし、ここで様々な問題が生じます。例えば、用いる数値解法次第では、計算にかかる時間が膨大になったり、数値解が発散して計算の続行ができなくなったりします。また、二つの異なる数値解法で計算した結果が全く違うといったこともあります。そこで、数値解析学では、数値解法の実現性や妥当性を数学的にきちんと評価し、さらにその議論に基づいて、より良い数値解法の開発を目指します。

数値解法には、NewtonやGauss、Eulerの名を冠したものも多く、数値解析学は、実はコンピュータが生まれる遥か以前から研究されてきた長い歴史を持つ研究分野です。ともすれば、数学的な研究は十分成熟しており、あとはコンピュータの発展に任せればよい、という印象を持たれるかもしれません。しかし、数値解析学ではまだまだ解決すべき課題は山積みですし、今後も、科学が多様化を続ける限り、解きたい問題も多様化し、それに伴い、数値解析学で議論すべき新たな課題もうまれてくるでしょう。

一言で数値解析と言っても、様々な分野がありますが、私は主に微分方程式に関連するテーマの研究を行っています。

1-1. 構造保存数値解法

微分方程式の数値解析も、Eulerの時代から研究されてきた古い学問分野で、実際に、常微分方程式に対するRunge-Kutta法や、偏微分方程式に対する差分法や有限要素法など、様々な解法が研究されてきました。特に、常微分方程式に対しては、数学者や数値解析学者によって、Runge-Kutta法のように対象の微分方程式を限定しない「汎用解法」についての数学理論が整備されてきました。実際、1980年代には、誤差解析・高精度解法の構築法・安定性などに関してかなり成熟した体系が整備されています。

さて、「汎用解法」理論が成熟してきた1980年代、「構造保存数値解法」という新しい研究の潮流が生じます。下の図1を見てください。これは、Keplerの二体問題を二つの数値解法で数値計算した結果です（一体は原点に固定してあり、もう一体の時間発展をプロットしています）。ここで比較している二つの解法は、（黒）Rungeの方法（Runge-kutta法の一種）と（青）Störmer-Verlet法で、「汎用解法」理論における精度は同じものです。厳密解は楕円軌道を描きます。左図は一周期弱数値計算したもので、若干の違いはあるものの、良し悪しが判断できるほどの違いは見られません。ところが、数値計算を続けていくと、右図のように大きな違いが現れ、Störmer-Verlet法の方が良さそうです。この違いを汎用解法理論で説明することは非常に困難ですが、 1980年代に、幾何的視点を導入することで、Störmer-Verlet法がうまく動く理由が解明されました。Kepler問題の時間発展写像はsymplectic性という幾何学的性質を有しているのですが、実は、Störmer-Verlet法はこの性質を厳密に引き継いでいるというのがその理由で（さらにその帰結として、Störmer-Verlet法はKepler問題に非常によく似た微分方程式を厳密に計算しているという解釈ができます）、これはRungeの方法をはじめ、ほとんどの汎用解法には見られない特徴です。

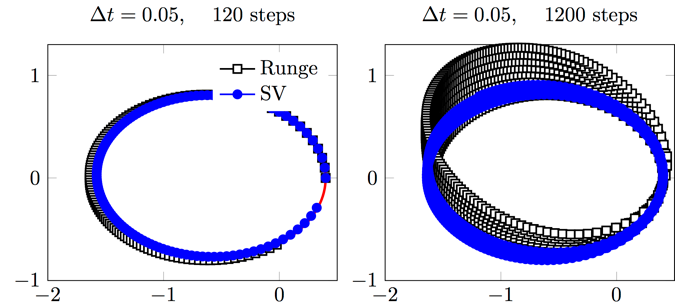
図1. Keplerの二体問題に対する数値解

Störmer-Verlet法のように、解きたい問題の数理構造を再現する数値解法のことを、総称として「構造保存数値解法」といいます。Symplectic性のようにしばしば幾何学的性質に着目するため「幾何学的数値解法」と呼ばれることもあります。 1990年代以降、常微分方程式に対する構造保存数値解法の研究は爆発的に進展しており、対象も幅広く、

・Hamilton系に対するsymplectic数値解法
・エネルギー保存解法
・勾配系に対するエネルギー散逸解法
・多様体上の微分方程式に対する構造保存数値解法（Lie群に基づく数値解法など）
・時間反転対称系に対する対称な数値解法
・高振動系に対する数値解法

など多岐に渡ります。近年では、偏微分方程式（Schrödinger方程式やMaxwell方程式など）や確率微分方程式にまで研究の対象は広がってきています。

私はこれまで、常微分方程式に対しては、エネルギー保存・散逸解法の理論の整備やそれに基づく新しい数値解法の開発を行ってきました。また、偏微分方程式に対しては、有限要素法の枠組みで構造保存数値解法の構築や拡張を行ってきました。さらに、非局所作用素を含む方程式にも興味をもっています。例えば、

Camassa-Holm方程式：u_t – u_xxt + 3uu_x = 2u_x u_xx + uu_xxx
Degasperis-Procesi方程式：u_t – u_xxt + 4uu_x = 3u_x u_xx + uu_xxx
Hunter-Saxton方程式：u_xxt + 2u_x u_xx + uu_xxx=0

といった方程式があります。このような方程式は、時間変数の偏微分と空間変数の偏微分が混ざっているため、通常の u_t=… といった形にしようとすると、積分のような操作をしなければなりません。そのため、見た目は微分方程式なのですが、ある点での時間変化を記述するためには空間領域全体の情報が必要になるため、「非局所」作用素を持つ偏微分方程式といわれています。このような方程式は、もちろん偏微分方程式論的にも大変興味深く1990年代から活発に研究されてきていますが、数値計算をする際にも「どのような解を捉えたいのか」など注意すべきことがたくさんあり、数値解法の構築は自明ではありません。そこで、筋の良い数値計算をするために、方程式の持つ構造に着目して、構造保存スキームを構築したり、その収束性の解析をしたりしてきました。なお、以上の多くは、松尾宇泰先生（東京大学），降籏大介先生（大阪大学），谷口隆晴先生（神戸大学），John C. Butcher先生（Auckland大学），David Cohen先生（Umeå大学）らとの共同研究に基づくものです。

1-2. 構造保存数値解法の新しい問題クラス

構造保存数値解法の研究ではまだまだ解決すべき課題はたくさんあります。例えば、現代科学で解きたい問題は、計算機の発展より遥かに速いスピードで大規模化しています。そのような問題に対して、数学的妥当性を維持し、かつ問題の数理構造を壊さずに問題サイズを小さくする方法が近年注目されています。しかし、まだまだ個別の研究例がほとんどであり、今後の発展が期待されます。

また、問題の特徴を抽出して、それに即した数値解法を作るという考え方は、微分方程式以外の数値解析でも有用です。例えば、行列やテンソルの近似分解に構造保存数値解法が貢献した例もあります。近年では、画像処理分野などであらわれる最適化問題との関連も指摘されています。なぜなら、多くの最適化問題の最適解は勾配系の平衡点として表現されるため、勾配系に対する構造保存数値解法の多くは最適化問題のアルゴリズムとして解釈できるからです。私の研究では、連立一次方程式の数値解法の幾つかが、実はある種の勾配系に対する構造保存数値解法に他ならないことを指摘し、その議論に基づいた新しい展開を目指しています（張紹良先生（名古屋大学），曽我部知広先生（名古屋大学）との共同研究）。

1-3. Uncertainty Quantification

自分自身の論文はまだないのですが、いま、一番興味を持っている分野です。微分方程式に限らず、数値計算結果は様々な誤差の影響で往々にして不確かなわけですが、その不確かさを数学的に評価し、信頼性の議論を行うUQ（uncertainty quantification）と呼ばれる応用数学の新しい一分野が形成されつつあります。

微分方程式の数値解析の立場からも課題が沢山あります。例えば、何らかの現象を記述する微分方程式に含まれるパラメータを、観測データをもとに推定したい状況を考えてみましょう。この場合、どのような推定手法を使うにせよ、大雑把に言えば、パラメータを少しずつ変えて微分方程式を何度も数値計算し、観測データにうまく合うパラメータを探します。このとき、観測誤差があるとすれば、必要以上に高精度な微分方程式の数値解法は不要かもしれません。だからといって雑に数値計算すると、観測誤差よりも微分方程式を数値計算する誤差が支配的になり、もっともらしい推定はできなさそうです。きっとどこかに落とし所がありそうですが、その際、経験的なものではなく数学的に明瞭な議論をしたいというのが問題意識です。

実はこの課題に対しては、直近の2、 3年の間に活発な研究がはじまっており、数値解にランダムに摂動を加えるというアイデアが提唱され、数学的な解析が行われたりしています。とはいえ、まだまだ個別の研究事例が中心ですので、統計学の研究者と協力しながら一般理論の確立に向けた研究を進めています。

2. 数値解析でつかう数学

数値解析学の研究では、実にさまざまな数学をつかいます。もちろん関数解析の基礎知識は必須ですが、幾何や代数、複素関数論などが必要になることもあります。これは、数値解析学の醍醐味でもあり、また、得意な数学があれば、研究をするうえで大きな武器になります。

私にとってこれまで一番衝撃的だったのは、常微分方程式の数値解法の研究で「木解析」がつかわれていることでした。 「木」とは連結で閉路を持たないグラフのことですが、常微分方程式の数値解析の専門書を開くと、

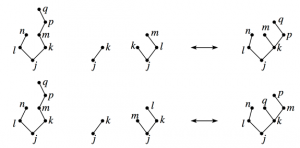
このような木がたくさん描かれています。なお、この図は、常微分方程式の数値解法についての定番教科書

E. Hairer, S.P. Nørsett and G. Wanner: Solving Ordinary Differential Equations I: Nonstiff Problems, 2nd ed, Springer-Verlag, Berlin, 1993.

からの抜粋です（翻訳版も出版されています）。さらに、木解析では群論などが登場し、代数的な議論が中心です。学部生のとき、グラフ理論と代数が特に苦手でしたので、非常にショックだったのですが、理解してみると非常に美しい理論でした。1960年代にButcherによって導入された「木解析」は、その後、常微分方程式の数値解析では必須のツールとなっていますが、さらに数値解析の枠組みを超えて、Hopf代数や理論物理学との関連なども指摘されています。数年前に、Butcher先生（80歳を超えてなお現役の数学者です!）と共同研究の機会にめぐまれ、数値解法の代数構造を大事にするという考え方に接することができたのは、大変貴重な経験でした。

3. 学生のみなさんへ

数値解析学は、高度な数学をつかったり、必要に応じてつくり出したりするという意味で数学の一分野ですが、同時に、研究を通して非常に様々な応用諸分野と関わることができ、非常にやりがいのある研究分野です。また、数値解析の研究では、数学とコンピュータの両立がとても重要です。もちろん、研究をはじめる段階で両方に十分な知識と自信がある必要はありませんが、両者を両立していく意欲がとても大事だと思います。かくいう私も、研究をはじめた頃は、数学は分からないことだらけで、プログラミングも苦手でExcelを立ち上げてしまうような状況でした。いまでも、論文でつかわれている数学が分からないことや、頭の中で数値解法が理解できてもその効率的な実装方法が分からないことは日常茶飯事で、日々勉強を続けています。