専門概要

主な研究対象は非線形の偏微分方程式です。ニュートンの運動方程式は、時間変数という一つの独立変数を持つ微分方程式ですが、時間変数と空間変数という多変数の独立変数を持つ微分方程式が偏微分方程式です。自然現象に現れる様々な相互作用を表す非線形項を追加して偏微分方程式を考察しています。非線形項を追加することによって、方程式の解が永遠に存在するか、あるいは途中の時刻で存在しなくなるかは一般に自明でなく、重要な解析対象になります。この解析において、実解析・調和解析・関数解析・関数空間論などの解析的方法を使用あるいは開発する必要があり、非線形偏微分方程式論は解析学における主要な研究分野の一つになっています。現在の現象から、未来の現象を予測したいという研究動機が背景にあります。

偏微分方程式の代表例としては、次のものがあります。

１．ラプラス方程式

２．熱方程式、複素ギンツバーグ・ランダウ型方程式。

３．波動方程式、クライン・ゴルドン方程式、ディラック方程式。

４．シュレディンガー方程式。

５．ナヴィエ・ストークス方程式。

６．アインシュタイン方程式。

上の方程式２は、熱などの拡散を表し、偏微分方程式の中で基本的な方程式です。３は音波や電磁波などの波の動きを表し、波が有限の速さで伝わることから、因果律が成り立つため、物理でも重用されます。４は量子力学における確率密度の伝播を表します。５は流体の動きを表し、熱方程式に対する技術が応用できますが、ベクトル場であることと非線形項の扱いの難しさから、ミレニアム懸賞問題に選ばれています。６は重力場を表し、波動方程式の技術が応用できますが、非線形項の扱いが難しい方程式です。１は、２～６において、時間依存しない定常的な場合を考察する際に現れます。

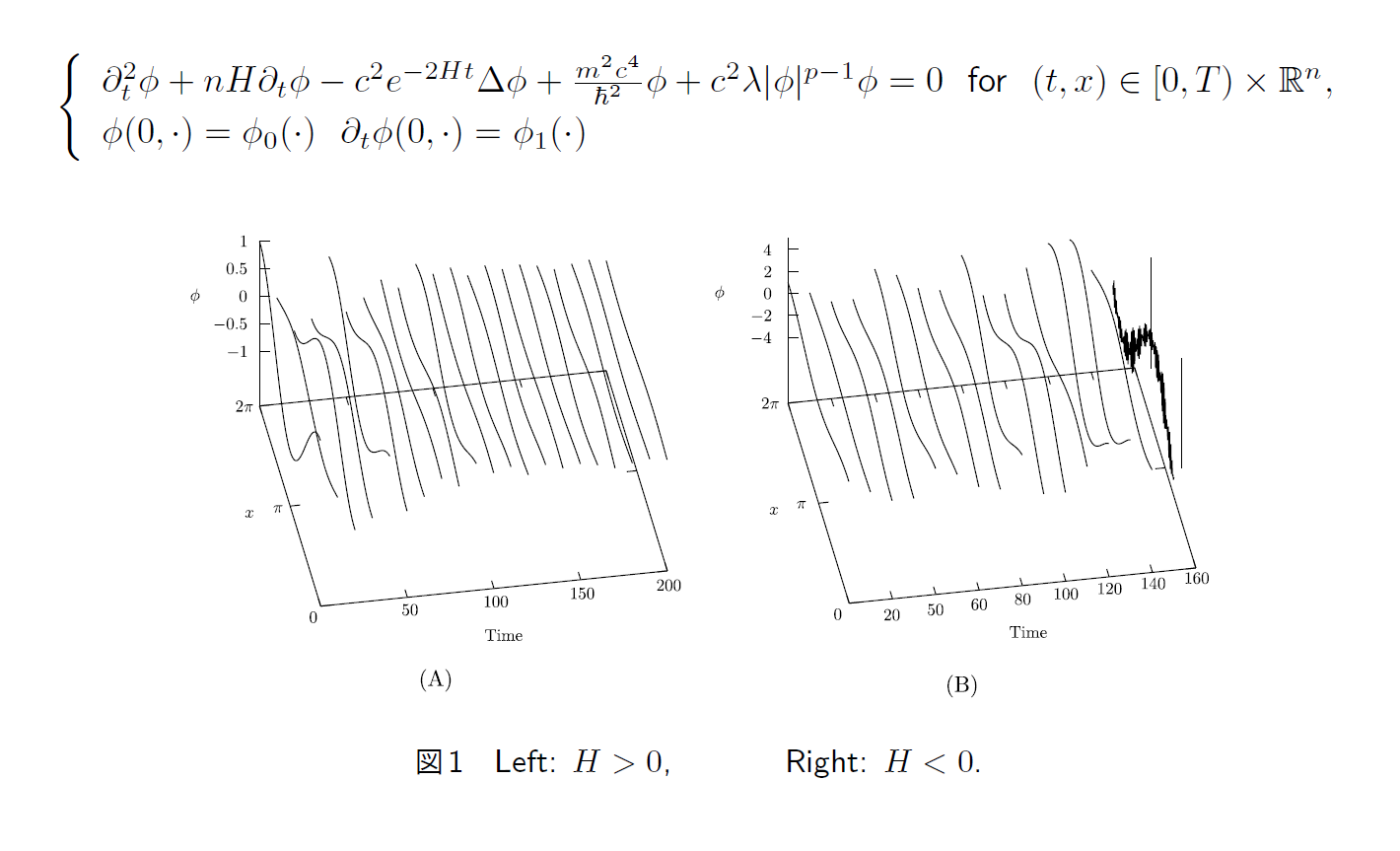
　１から５までの方程式は、我々が居る時空における現象を表します。６のアインシュタイン方程式も時空における重力を表しますが、方程式の解は我々の時空そのもの、つまり宇宙を表します。６の方程式の解が安定して存在するかどうかを調べることは、我々の宇宙が安定して存在するかどうかを調べることになります。微分方程式が宇宙の時間発展まで表現できることは驚きです。空間に特別な位置は無く、空間は等方的であるという仮定の下では、６の方程式は高校生でも解ける簡単な微分方程式になります（福江 純著「完全独習現代の宇宙論」（講談社）参照）。しかし、そのような仮定がない状況では、高度な技術を要する複雑な微分方程式です。この方程式が1916年頃に発見されて以来、物理学的研究と共に、アインシュタインの居たプリンストン大学を一つの中心として、偏微分方程式論的研究が行われました。1980年台と2000年台には非線形項の構造解明に大きな進展が見られ、時間大域的解の存在が部分的に示されるようになりました。更に、1998年には宇宙の加速膨張が発見され、その原因がダークエネルギーと呼ばれています。ダークエネルギーは、アインシュタイン方程式における宇宙項と呼ばれる項に対応しており、膨張宇宙あるいは収縮宇宙の研究が改めて重要になっています。宇宙の誕生間もない頃、あるいは今後遠い将来、我々の宇宙は急速に膨張すると考えられているからです。ダークエネルギーの正体は物理学的に研究されている所ですが、それによる効果を数学的に解明する研究も行われており、私も取り組んでいる課題です。現在は、アインシュタイン方程式の解である膨張あるいは収縮する空間において、非線形項が付いた上記の１から５までの方程式を考え、解が存在するかどうかを調べています。空間の膨張と収縮ならびに非線形項の構造が、解の存在にどのように影響するかを解明し、膨張と収縮の効果を数学的に特徴づけることが目的です。空間の膨張あるいは収縮によって、非線形クライン・ゴルドン方程式に修正項が生じますが、空間が膨張する場合に、この項を消散効果として評価し、方程式の解が安定的に存在することを示しました（2014）。例えば、ド・ジッター時空と呼ばれる膨張あるいは収縮する空間における非線形クライン・ゴルドン方程式は以下のものになります。方程式の解の時間発展を数値シミュレーションしたものが、その次になります。左側のシミュレーションは空間が膨張する場合の波の形状を示したもので、右側は空間が収縮する場合を示しています。左から右へ時間が経つに連れて、空間が膨張する場合は、波の凹凸が急激に消散する様子を表し、空間が収縮する場合は、波の凹凸が急激に増長する様子を表しています（2019）。このような数値シミュレーションと共に理論研究に取り組んでいます。

４年生セミナーについて

よく使用するテキストは次になります。

(1) 堤 誉志雄著、偏微分方程式論、培風館。

(2) 井川 満著、双曲型偏微分方程式と波動現象、岩波書店。

(3) L. C. Evans著, Partial Differential Equations (2nd Edition), American Mathematical Society.

(4) T. Cazenave著, Semilinear Schrödinger Equations, Courant Lecture Notes In Mathematics.

いずれも偏微分方程式についての入門書です。平易な記述で読み易く、基礎力を養成するのに適しています。学生の希望、あるいは大学院進学を見込んだ将来計画を考えて選択します。１は、フーリエ級数や超関数などの知識を紹介した後、非線形シュレディンガー方程式の初期値問題と解の性質について解説しています。セミナーでは、この非線形シュレディンガー方程式を主に考察対象とします。2は、偏微分方程式の典型の一つである双曲型方程式について、導出方法、解の存在、解の漸近挙動について解説しています。セミナーでは、解の存在定理に重心を置いて、読み進めます。3は、国外でよく使用される教科書で、偏微分方程式の取り扱い方法を広く解説しています。セミナーではPart IIIの変分法及び非線形波動方程式を主に考察対象とします。４は非線形シュレディンガー方程式についての教科書で、ソボレフ空間における時間大域解と爆発解について解説しています。本書を読み進めれば、論文執筆の基礎が出来ると思いますので、後は幾つかの論文を読む段階へ移れるでしょう。偏微分方程式について、簡潔に概要を知りたい方には、３年生でも読むことが出来るものとして、渋谷 仙吉・内田 伏一共著「物理数学コース偏微分方程式」（裳華房）が挙げられます。ラプラス方程式に関心がある場合には、田中 和永著「変分問題入門―非線形楕円型方程式とハミルトン系」（岩波書店）、鈴木 貴・上岡 友紀共著「偏微分方程式講義 半線形楕円型方程式入門」（培風館）、I. Kuzin S. Pohozaev 共著「Entire Solutions of Semilinear Elliptic Equations」(Birkhäuser) を使用することがあります。

　セミナーでは、本の内容理解を中心として、解説する能力の向上を目指します。この能力は、将来、数学のみならず広く役立つことでしょう。偏微分方程式は、数学的面白さと共に、物理、情報、気象、地震、金融などへの広い応用があります。微分方程式に習熟していなくても、配属後に興味に応じて勉強すれば支障ありません。

　４年生では、就職か大学院進学かで悩む方もいらっしゃることと思います。経済的な理由や自身の適性についての不安もあるかと思いますが、大学院の少人数教育で真摯に研究と伝達能力の向上に取り組むと、学生は著しく成長します。不安な点や不明な点があればメールで連絡して下さい。

大学院セミナーについて

　修士課程のセミナーは、週に一時間から二時間程度です。一年目は、上記の(3)や(4)などの偏微分方程式についての基本的な英語の書籍を勉強しつつ、夏頃から基礎的な論文の読み込みへと移行していきます。ソボレフ空間の性質について書かれたJ. Bergh, J. Löfström共著「Interpolation Spaces: An Introduction」（Springer）をよく使用します。書籍や論文を読み込み、分かり易くセミナーのメンバーや教員に伝えることが求められます。一学年で二名程度の少人数でのセミナーになりますので、時間をかけての準備が重要です。不明な部分は、メンバーに相談したり、書籍で調べたりする必要がありますが、その上で不明点について説明して下さい。どのように考えて何を調べるかという過程が重要です。二年目は、読んでみた論文を基に、改善個所を考えて新しい結果が出るように試行錯誤と創意工夫を繰り返します。秋頃には、修士論文の作成を始め、取り組んだ課題について整理して記述すると共に、自分で調べた数学的知識を付録として記載します。修士論文発表会の一ヵ月位前からは発表練習を行います。この段階では、簡潔に効率よく、分かり易く発表することが求められ、使用する資料や言葉などを考え抜く必要があります。セミナーの準備の仕方については、河東泰之先生の次のホームページに心構えが記載されています。そこまでを要求する訳ではありませんが、参考になる点は多いです。

https://www.ms.u-tokyo.ac.jp/~yasuyuki/sem.htm

　博士課程のセミナーは、基本は週に一時間から二時間程度ですが、研究課題の進捗状況に応じて、頻繁に行うこともあります。論文作成に取り組む以外にも、他研究室のセミナーや、研究集会に参加することもあります。他大学の教員や大学院生との交流により、視野が大きく広がることでしょう。一年目から三年目まで、研究の進捗は学生それぞれで異なります。結果が思うように出ない場合もあり、適性について思い悩むこともあるかも知れません。意思を強く持ち、こつこつと自分の出来ることを広げていくのが賢明と思います。

高校生の方へ

　オープンキャンパスや体験授業でよく聞かれる質問として、数学の適性があります。高校までの数学と大学の数学が、大きく異なることは知られているようで、不安に思うのはもっともです。数学の研究者は独自の個性を持つ方が多いので、様々な回答があると思いますが、私は次をアドバイスしています。高校の数学で、新しい考え方や工夫を良く理解し、問題を解く際に、それらを自分なりの方法で用いて、納得する解答を目指しているならば、大学においても大きな支障は少ないでしょう。また、数学的な考え方が性に合っているならば、数学科に入学してから、興味のある分野を選べば良いでしょう。大学の授業では、数学における言葉の定義をよく理解し、証明を論理的に理解する作業が多く求められます。数学に限らず、野球でいうところのエースと四番は天性のものがあるかも知れませんが、強い意志を持って、自分なりに創意工夫する姿勢が大事かと思います。

一般の方へ

　「数学は役に立つのか？」とは、よく聞かれる質問です。1990年半ば位までは、数学科を卒業した場合の進路先は、高校の教師、企業のプログラム・システム関係、品質管理、保険、銀行が一般的でした。近年では、情報技術における数学的理論の活用が大きな競争力・利便性・収益を生み出すようになったことから、数学科卒業の学生はセキュリティー、金融、データ活用にも開がり、就職はかなり良い状況です。すぐに役立つものは、廃れも早いですが、数学の抽象性はすぐには役立たずとも長く役立つものです。解決すべき問題に対して、幾つかの場合分けを行いながら、資料を調べて論理的に最適解を見つけ出す作業は、数学を学んだ方が得意とすることの一つです。国語が社会の言語とすると、数学は自然の言語と言えます。何かしら起こる現象を、論理的かつ誰でもその気になれば理解できる形で表現したものは、○○数学あるいは数理○○学という形で体系化されることが多くあります。数学は演算規則に限らず、現象を論理的に表現し、皆で発展させるための優れた方法論の一つです。数学もしくは数学的思考が、社会の発展に目で見える形で寄与する時代になっており、その素質が求められる時代でもあります。

研究者の方へ

　情報科学研究科内での数学専攻として、主に研究環境を紹介したいと思います。本専攻は吹田キャンパスにあり、万博記念公園の北側に位置します。大阪モノレール阪大病院前駅から徒歩10分程度の位置で、大学本部の目の前にあります。広大な敷地に多くの研究施設が敷地に余裕をもって建っており、緑が多く、キャンパス内を歩く場合は、スマートフォンの地図アプリがないと迷う可能性があります。その分、研究の息抜きの散歩には開拓心がそそられます。足を延ばせば、南東に万博記念公園、北西に大きな池のある千里北公園があり、来訪者と散策あるいは一人で思索に耽ることができます。福利厚生施設が充実しており、情報科学研究科棟１階に小さめのセブンイレブンと食堂がある他、カフェやレストランも近くにあります。吹田キャンパス近くは、北側遠方に山々が連なる麓に住宅街が広がっており、晴天が多いこともあって綺麗な街並みが見られます。モノレールと電車の利便性も良く、京都大学を始めとする近隣大学を訪問するのも比較的容易です。
　本専攻は、豊中キャンパスにある理学研究科数学専攻を母体として設立されたことから、理学研究科数学専攻とは密に連携しています。例えば、研究内容は理学研究科数学専攻でも紹介されており（ http://www.math.sci.osaka-u.ac.jp/staff.html ）、理学部の講義と４年生セミナーも担当しています。理学研究科棟への入棟にも便宜が図られています。
　本専攻は情報科学研究科内にありますが、研究内容として、情報科学に密接に関わる数学を行わなければならないという訳ではありません。現在の情報化社会において、情報の伝達・保護・活用に関する数学あるいは数学的思考の重要性は広く認められており、本流の数学を研究し教育できる研究者が求められていることが背景の一つと思います。私の場合は、波動方程式の研究が情報の伝達に関わるため、数学的理論研究と数値計算を通して、情報に関わる研究者との交流ができればと考えています。
　専攻内の雰囲気は、新しい建物内で落ち着いていて静かです。疲れた時に、専攻事務室で雑談やコーヒーを入れて休憩しています。大学院生室は狭過ぎず、広過ぎずで、一人で研究しつつも他の院生と自然とコミュニケーションが取れるような広さです。教員居室との距離も近く、より賑やかに大学院生活が送れるよう院生を迎えていきたいと思います。
　大阪に異動する前に、何人かの先生方から大阪は良い所との言葉がありました。空港・鉄道・高速道路の利便性、緑多い住環境、豊富な研究施設と充実した研究環境の他に、人の好さも感じられます。
　次の写真は情報科学研究科棟から見た大学本部（煉瓦色）です。西尾総長は、元情報科学研究科長です。その奥に医学部と附属病院（灰色）が見えます。

略歴

• 1996年　日本学術振興会 特別研究員(DC1)
• 1999年　東北大学 大学院情報科学研究科 助手
• 2005年　東北大学 大学院理学研究科 助教授（のち准教授）
• 2013年　山形大学 理学部（のち学術研究院） 教授
• 2022年　大阪大学 大学院情報科学研究科 教授

連絡先

• E-mail ： makoto.nakamura.ist@
• Tel ： 吹5895 (06-6105-XXXX)

4ケタの電話番号は、大阪大学での内線番号です。
メールアドレスは、末尾の"osaka-u.ac.jp"が省略されていますので、送信前に"osaka-u.ac.jp"を付加してください。