■CREST研究に関する情報

●大阪大学大学院情報科学研究科 JST-CREST 杉山由恵 (研究情報) 

● https://syue0120.wixsite.com/sugiyama

授業動画（porous medium equations, Keller-Segel systems）

● 授業動画（porous medium equations, Keller-Segel systems）

■“微分方程式を基盤とした数学研究”への期待

　自然法則は関数に微分を作用させた項を含む方程式（微分方程式）で記述されること が通常です。微分方程式の例として、質点に関する運動の第２法則（ニュートンの運動 方程式）を学習したことがある方も多いことと思います。 　微分方程式で記述される自然現象は多種多様です。例えば飛行機が運航時に作り出す 空気の流れは“流体の（連続方程式と）運動方程式であるNavier-Stokes方程式”で記述 されています。この－Navier-Stokes方程式－は、世界中の多くの研究者によって数 学解析され、その過程において新しい数学の枠組みや理論が開発される等、数学発展へ の貢献の多大な方程式です。 数学分野に留まらず、理学・ 工学・ 医学分野の科学者を魅了してやまないNavierStokes方程式です。その一意可解性問題はクレイ数学研究所によって2000年に提唱 され、100万ドルの懸賞金もかけられている７つの数学問題のひとつに挙げられています。

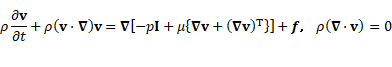
ミレニアム問題：ミレニアム問題：任意に与えられた初期条件に対して、Navier-Stokes方程式は時間 大域的な一意正則な解を有するか？ 興味のある方には、是非、ミレニアム問題に関する記事に目を通して頂きたいと思いま す。（例えば、以下をご参照下さい。） https://matome.naver.jp/odai/2134641375620843001

　その他の興味深い例として、生命現象を記述する偏微分方程式数理モデルがあります。ヒト体内の生命維持には血液細胞の一種である白血球の働きが欠かせません。ある種の白血球はバクテリアを貪食し、体内の殺菌を行っています。このような生命現象もまた「白血球の個体密度」や「白血球走化性を惹起する誘引物質の濃度」を未知関数とした微分方程式を用いて記述されます。

　では、流体現象や生命現象をNavier-Stokes方程式や走化性方程式といった微分方程式を用いて記述すると、どのようなアウトプットを期待できるのでしょうか。実は、流体や細胞運動の時経変化を予測する、つまり、未来を予見することが可能になります。微分方程式を駆使すれば、初期時刻での個体密度等を情報（初期条件）として与えることで、時間発展した後のそれらの様態（解構造）を知ることが出来るのです。

　現象について、今後起こりうる様態変化を予測したい、これは自然な欲求です。微分方程式を上手に活用することで、こうした要望に応えることが可能になるのです。

　微分方程式に基づく数学研究は、関数解析的手法、実解析的手法、数値解析的手法、変分法的手法、接合漸近展開法、等のさまざまなアプローチにより、自然界や生体内の興味深く、神秘的で多様な現象について、未来予想図を描くことを可能にしてくれます。更にそれらは、自然現象解析や生命現象解析に留まらず、社会計画・医療機器開発・贋作鑑定・効率の良い広告活動の選定等にも有効です。

　これらはほんの一例であり、実際、微分方程式により自然科学、工学、社会現象等で解明される事例は、列挙に暇がありません。最近では、社会における支配原理・法則が明確でない諸現象を数学的に記述・解明するモデル創出を目的としたJSTプロジェクトも数学協働領域に設定されています。このように、近年、数学分野の研究者等が自らの研究領域を超えて、自然科学、情報科学、工学、生命科学の理論や実験の研究者等と連携することの重要性の認識が進み、連携を潤滑に進めていく基盤が整いつつあります。

　今後、数学解析の進歩に立脚し、微分方程式を活用した異分野融合型研究が発展していくことで、我々の生活はより豊かになっていくことでしょう。

■　私の従来からの数学研究

　数理生物学の基礎方程式を中心とした非線形偏微分方程式を研究対象としています。研究手法としては、関数解析学，調和解析学等を採用しています。

　解の時間局所・大域的存在と一意性、正則性、安定性に加え、空間時間変数に関する漸近挙動解析や特異性解析が主たる研究テーマです。

　解の存在・一意性・安定性は方程式の“適切性”とよばれ、偏微分方程式論の基本的な問題意識です。私は、走化性方程式を中心に、適切性解析の研究に従事しています。加えて、特異性解析も研究対象としています。具体的には、非線形方程式特有の現象である解の有限時間爆発とその（有限時間・無限時間）漸近挙動を、関数解析学的アプローチにより解析しています。更に、関数のクラスを測度値解まで広げることで可能になる、“大きい初期値を持つ解の時間大域的構造”を明らかにしようとしています。上述の数学解析を通じ、移流項を有する拡散方程式に関して、移流と拡散のバランスに指標を導入した統一理論を構築することを最終目的としています。

■　私の近年の研究興味

　構築された数理モデルについて「数学問題を設定して解く」ことは数学研究者にとって最も重要な研究課題です。一方で、「現象を発見すること」が、物理学研究者にとって最上位課題であるということを見聞きします。

　「数学問題を設定して解く」と「現象を発見する」の間に数理モデル構築があります。現在、私は生体内現象、特に血栓を疾患対象として偏微分方程式数理モデルを構築しています。

　同モデルに基づく数値シミュレーションを通じ、医療機器開発に繋げようとしています。より具体的には、脳動脈瘤の治療シミュレータ開発を目指しています。数学研究者が医療機器等の実用化を試みるとき、分野横断型・異分野融合型研究が欠かせません。学際的研究を推し進めながら、数学研究では出逢わない苦難や喜びに、気づきや発見の多い日々を送っています。

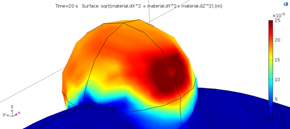
みずほ情報総研の高山務氏との共同研究

■　数学・数理科学への期待

　多光子顕微鏡の開発等、生体内の撮影技術は日進月歩です。将来的には、生体内を空間3次元動画で鮮明に映し出せる日が来るかもしれません。現在の工学技術では、空間2次元については、この期待に十分に応えています。一方で、空間3次元については、今後の進歩が待たれるところです。

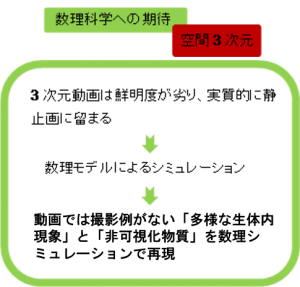
　数理科学の強みは、動画では撮影しきれない現象を（仮説に基づいて構築された）数理モデルを用いることで、多様にかつ容易に再現出来ることにあります。医師の経験や医学論文を通じて得られた知見を基に仮説を立てることで、実行される数値シミュレーションを、より実現象に近づけていくことが出来ます。

■　研究者の道へ

　現在、数学研究や科学研究に魅了される日々を送っています。私が数学を専門分野として研究者を目指そうと考え始めたのは、高１の春（16歳になって間もない３月）でした。中学時代は弁護士に憧れていましたが、高校時代の国語の先生から京都大学博士課程に籍を置く教え子の研究生活の様子を聞かせて頂くうちに「博士課程進学」への憧れを募らせていくようになりました。

　大学卒業後、早稲田大学大学院に進学した後、数学研究者を目指した生活が始まりました。早稲田大学（助教）・津田塾大学（准教授）・大阪市立大学（教授）・九大数理学研究院（教授）勤務を経て、2018年4月に大阪大学情報科学研究科に着任致しました。

　研究者人生で、最初の転機となったのは、指導教官（早稲田大学）との出逢いです。指導教官の言葉で最も印象に残っているものは「君にはPassionがある」です。時を経て、私も博士課程の学生さんを指導する立場になりました。Passionのある学生さんに出逢うとき指導教官がおっしゃって下さった言葉を思い出します。第二の転機は、津田塾大学勤務４年目に頂いたサバティカルリーブ（研究休暇）です。ヨーロッパでの一年間の滞在（ドイツ・スペイン）では、年齢も国籍も異なるLuckhaus教授（背の高い青い目のドイツ人・Max Planck 研究所）との素晴らしい出逢いがありました。数学を通じてLuckhaus教授との間に生まれた絆は、永遠に変わることがないと信じられる私の人生の財産です。

数学を通じて繋がる関係は、深くて強いものです。素敵な出逢いは、次の素晴らしい出逢いを呼び寄せてくれるようです。私の場合はLuckhaus教授がVelazquez教授（ スペイン人・Bonn大学） に、Velazquez教授がCarrillo教授（ スペイン人・Imperial College London）に。こうして国籍を超えて友情が広がっていきました。

■　大阪での二度目の勤務

　津田塾大学勤務時の居住地は池袋で、大阪市大勤務時は心斎橋に、九州大学勤務時には天神近く、現在は、梅田近くに居住しています。2011年から2012年には、大阪市立大学にて教鞭をとりました。この頃は、心斎橋のパーソナルトレーニングジムに通っていて、心温まる思い出をたくさん持つことが出来ました。2018年からは二度目の大阪での勤務が始まっています。これから、多くの思い出が築かれていくことを楽しみにしています。

■　博士学生さんとの関わり

　九州大学時代は、学生さん達から、毎年Happy Birthdayを祝ってもらいました。写真は彼らからのプレゼントです。

　九州大学時代は、Healthy Labを目指して、研究室にトレーニングマシーンを置いていました。九州大学着任と同時に、私が指導を開始いたしました学生さんが一名います。数学と体力を共に鍛え、2018年3月には博士号を取得しています。

　数学研究とともに、学生指導・後進の育成に尽力していきたいと思っています。

【近年の主な業績】

1. Carrillo J.A. and Sugiyama Y, Compactly supported stationary states of the degenerate Keller-Segel system in the diffusion-dominated regime, Indiana University Mathematics Journal (in press).
2. Kawakami T and Sugiyama Y, Uniqueness theorem on weak solutions to the Keller-Segel system of degenerate and singular types, Journal of Differential Equations, 2016, 260, 4683-4716.
3. Kozono H, Miura M, and Sugiyama Y, Existence and uniqueness theorem on mild solutions to the Keller-Segel system coupled with the Navier-Stokes fluid, Journal of Functional Analysis, 2016, 270, 1663-1683.
4. Sugiyama Y, Partial regularity and blow-up asymptotics of weak solutions to degenerate parabolic system of porous medium type, Manuscripta Mathmatica, 2015, 147, 311–363.
5. Miura M and Sugiyama Y, On uniqueness theorem on weak solutions to the parabolic-parabolic Keller-Segel system of degenerate and singular types, Journal of Differential Equations, 2014, 257, 4064-4086.
6. Sugiyama Y, Tsutsui Y, and Velázquez J.J.L., Global solutions to a chemotaxis system with non-diffusive memory, Journal of Mathematical Analysis and Applications, 2014, 410, 908–917.